setrfull.blogg.se - Quadratic sequence

So Pattern D does not have a step with 167 tiles.

We'll check if Pattern D has a step with 167 tiles by attempting to solve $$(n+3)^2=167.$$ But if this were true, 167 would need to be the square of $n+3$, and $167$ is not a perfect square.

In part (c), students have an opportunity to express regularity in repeated reasoning (MP.8) by applying these same "undoing" operations to an equation to isolate a variable of interest in terms of other variables. The equations in this particular task highlight algebraic moves that are useful when students learn to solve quadratic equations by completing the square. The purpose of this task is to motivate solving a quadratic equation where the variable of interest, $n$Â can be isolated by "undoing" operations. Or students could be asked to discuss how they "see" the pattern growing ( here is a good primerÂ onÂ what that might look like.)Â Or, they could be asked to evaluate d(1) and explain its meaning in terms of the number of tiles in Pattern D.

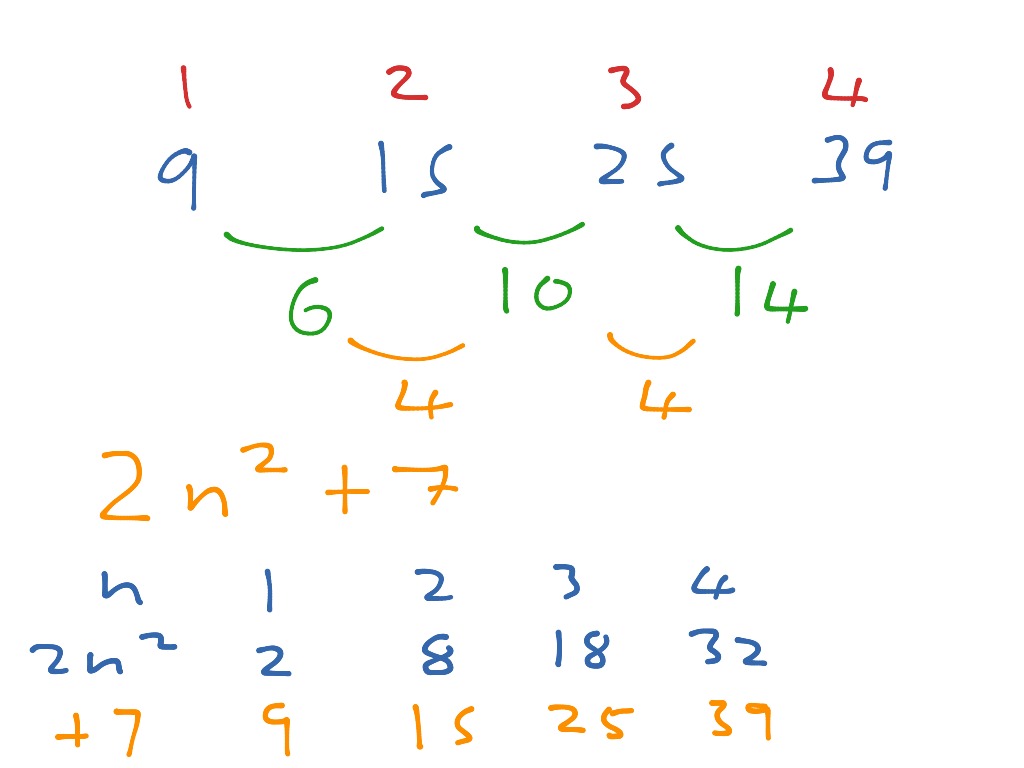
For example, they could be asked to "draw the next step" for one or more patterns. If not, students might benefit from additional questions to familiarize themselves with the idea. Ideally, students will have had some experience working with visual patterns prior to this task. That the domain of these quadraticÂ functions isÂ the set of positive integers provides an interesting wrinkle which students might not be used to thinking about in the setting of quadratic functions.Â The functions roughly increase in complexity through the threeÂ tasks, with the intent that the techniques learned in each will be used and expanded in the subsequent tasks.Â The other tasks in the sequence are Quadratic Sequence 1Â and Quadratic Sequence 3. However, seeing structure is emphasized in the standards because of how it connects and helps inÂ understanding many foundational concepts, and these tasks develop the ability to see structure when working with quadratic expressions and equations.

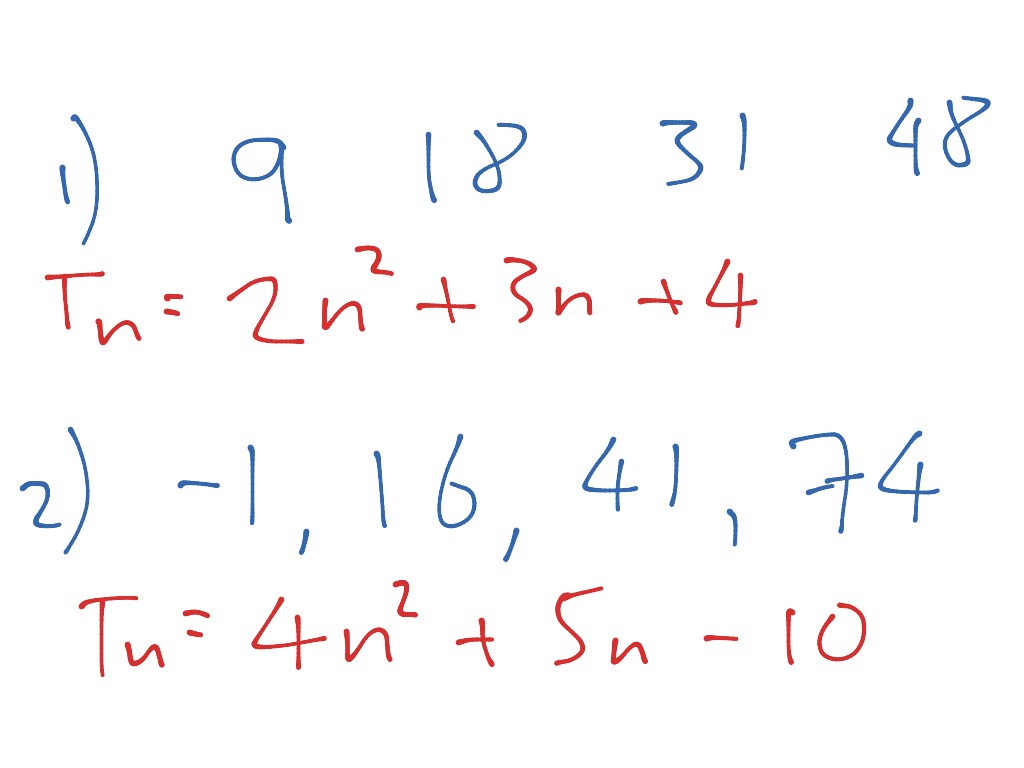
Students are asked to analyze the functions in the context of questions about the sequence of figures, a process which involves manipulating the quadratic expressions into different forms (identifying square roots at first, then completing the square in the third task.)Â With solving quadratics, there can beÂ an impulse to put everything in standard form and just use the quadratic formula.

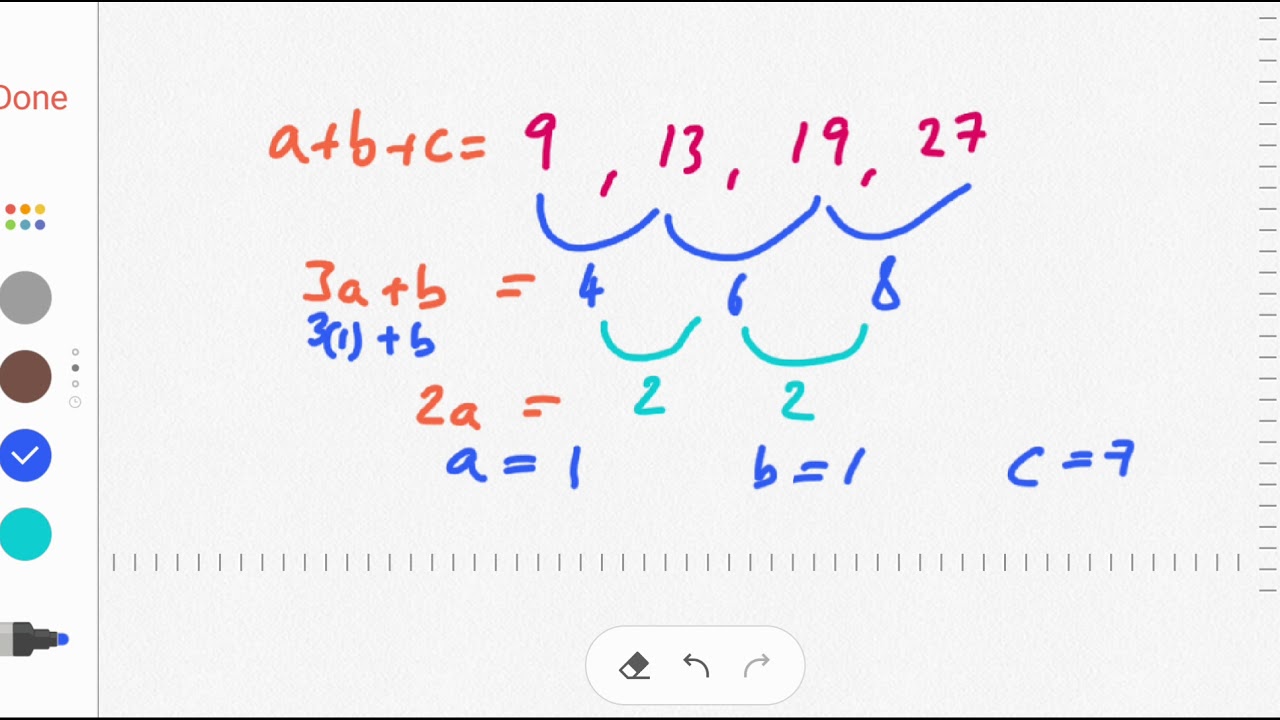
This task belongs to aÂ series of threeÂ tasks that has students process a sequence of tile figures with the property that the $n$-th figure in the sequence has $f(n)$ tiles, for some quadratic function $f$.